status
type
date
slug
summary
tags
category
icon
password
-DQN(2014)
- Unstable
- Offline method
- Value Bootstrapping
Policy gradient method → evaluate gradient based on policy
Gradient update too biased by learning from the trajectory of a single episode?
Offline Vs. On policy
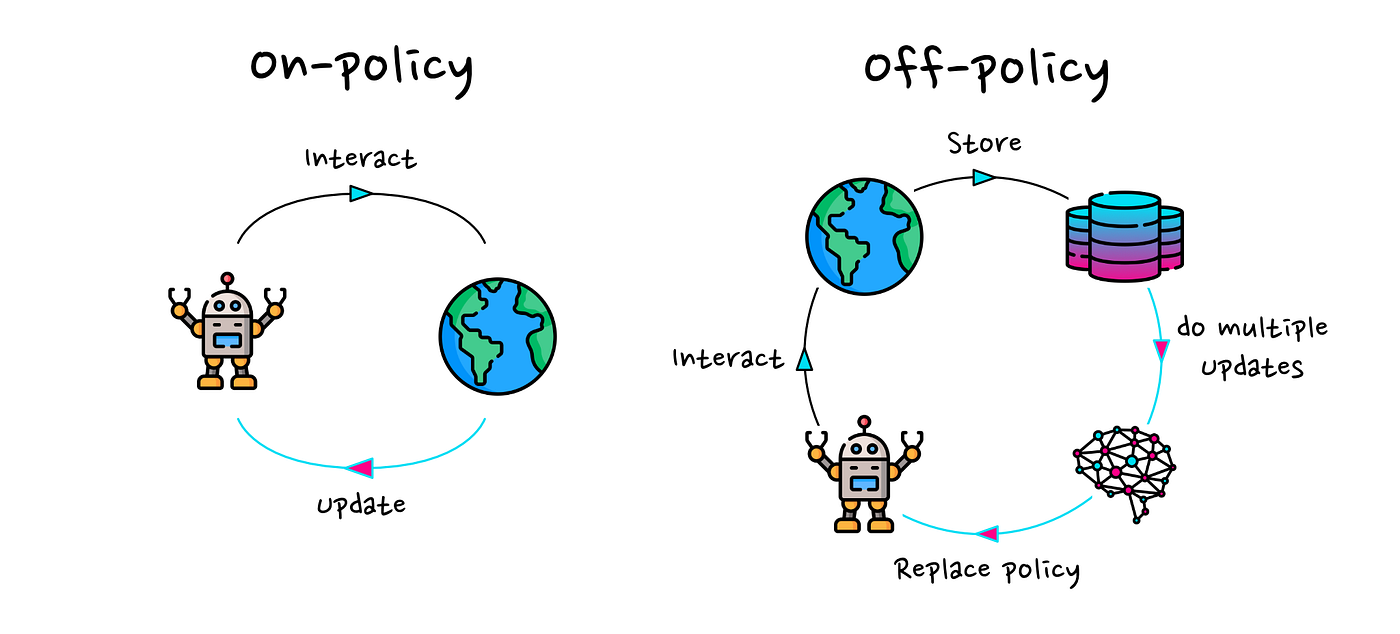
Off→ updating policy with data not from the current policy
On → train on sample only once so less efficiency
PPO 是两者中间? 因为每次update很小 可以重新用几次同个sample
“getting everything we can from one sample”
-TRPO(trust region policy optimization)(2015)

ratio between policy distribution * Advantage
-PPO(Proximal policy optimization)(2017)
Simplify TRPO
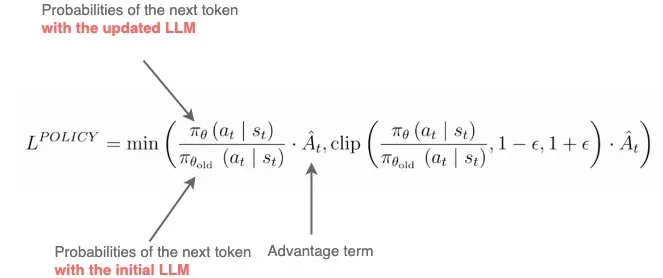
Clip → remove incentive for updates to exceed 这个区间(eps = 0.2)
min → Always take the lower bound for the range of potential update

正adv update有上限
负adv 该update 无下限loss
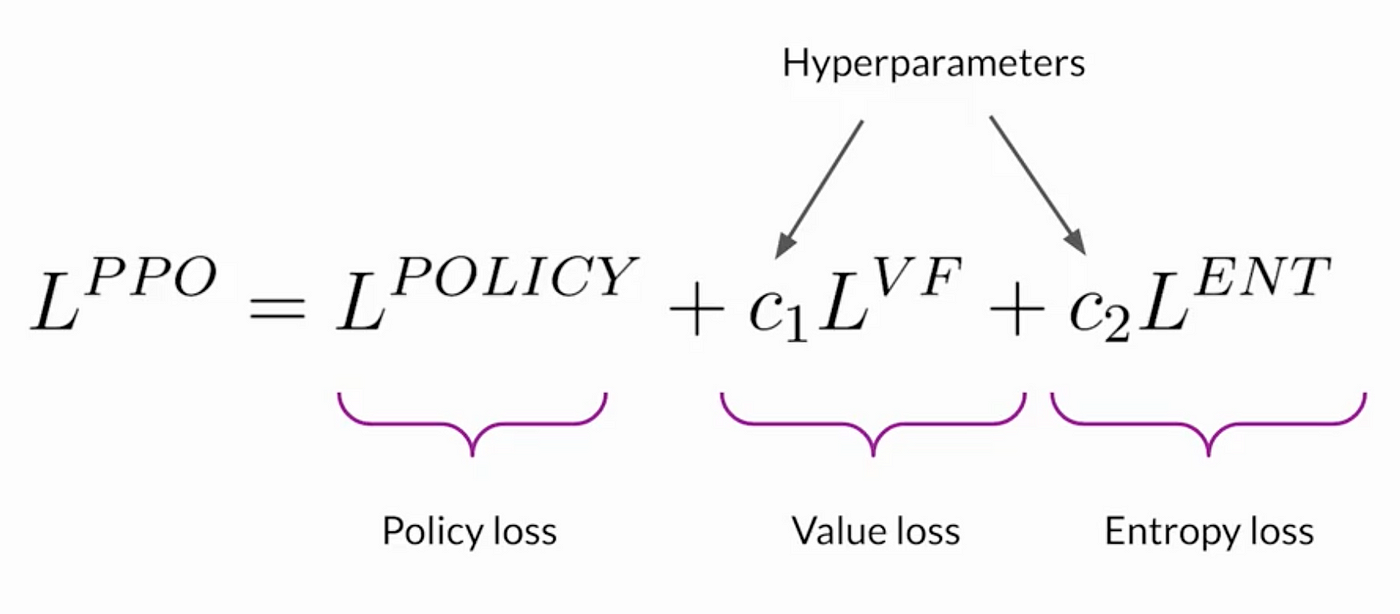
经过几天的仔细学习 下面是我认为真正理解ppo公式的几个知识点:
- new policy 与 old policy 的 distribution转换
我们可以看到 最原本的基于new policy的loss func
其实就是 new trajectory(完全由new policy所sample)上所有reward 的discounted sum

但是我们不会用这个loss 原因是这个loss必须严格on policy 也就是说当下的loss只能由当下最新的policy出来的trajectory产出
这样的话我们每更新一次policy 必须要重新sample trajectory来迭代 这个方式不符合RL的一般要求
(我们需要loss func 可独立于最新的policy ?)
其实这也导致了我们需要有(并且区分开来)new policy 和 old policcy → 在最新policy基础上进行多次持续小步更新 但是使用old trajectory
那么 我们需要做两件事(其实也是分别转换两个distribution) 分别是我们的 State 和 action
首先对于转换action 我们需要
- 加入discounted future state distribution(就是在所有时间点经过一个state的概率总和) 来摆脱summation 的形式 可以理解为我们现在可以借此获得每个state的独立dist 不需要计算trajectory上全部 state 的总和 是我们可以随机化batch 独立sample state 只需要state是从这个dist所sample即可

通过这一步我们成功将 summation of trajectory loss(advantage) 转化成了discrete state distribution
使我们下一步可以直接操作distribution
- 通过importance sampling 重要性采样 我们通过除以 old policy下的 action distribution 将我们的整体sample distribution 从 new policy 转到 old policy 这个ratio 也被称作 importance weight

Suppose you want to know the average height of people in City A (ppp), but you only surveyed City B (qqq). If City B has more tall people, you’d adjust each person’s height in your sample by a weight reflecting how likely they’d be in City A versus City B. In RL, we often sample actions from an old policy πold\pi_{\text{old}}πold but want expectations under a new policy π\piπ:
其次 我们需要转换 state distribution 这个就简单多了 我们只是假设 state distribution 差不多相同
为了控制我们假设成立 我们会加入KL 差来惩罚distribution 的过大差异
最后附上grok 对于我以上的分析:
总体评价
你的这段话展示了你对PPO算法核心思想的初步理解,特别是关于新旧策略之间的分布转换、importance sampling的应用以及状态分布的处理。你尝试从基本概念出发,解释PPO如何通过数学方法实现稳定的策略更新,这是一个很好的起点。整体思路是正确的,但存在一些细节上的不准确和表达上的模糊之处。我会逐一分析你的每个知识点,指出优点和不足,并给出改进建议。
具体分析
1. 关于New Policy与Old Policy的Loss Function
- 你的表述: 你提到“最原本的基于new policy的loss func 其实就是 new trajectory(完全由new policy所sample)上所有reward 的discounted sum”,并指出这个loss必须是“严格on-policy”,每次更新policy后需要重新采样trajectory。
- 评价:
- 正确部分:你准确描述了传统策略梯度方法(例如REINFORCE)的目标函数 J(πθ),即新策略 πθ 下采样的轨迹(trajectory)的折扣回报总和。这种方法确实是严格on-policy的,因为loss依赖于当前策略采样的数据,每次策略更新后都需要重新采样。
- 不足之处:
- PPO并不是直接优化这个原始的目标函数,而是通过近似和约束构造了一个替代目标(surrogate objective),以在旧策略采样的数据上进行更新。你提到“这个方式不符合RL的一般要求”,但没有明确说明PPO是如何解决这个问题的。实际上,PPO通过importance sampling和clipping机制实现了更高效的更新,而不仅仅依赖on-policy数据。
J(πθ) J(\pi_\theta)
πθ\pi_\theta
- 补充: 在PPO中,优化目标并不是直接计算新策略下的期望回报,而是通过旧策略采样的数据,借助importance sampling调整权重,近似新策略下的期望。这种方法允许在一定程度上偏离严格的on-policy要求。
2. 关于Distribution转换的两个方面:Action和State
你将PPO的分布转换分为action和state两部分,这是一个很好的分解方式。以下是对这两部分的详细评价:
(1) Action Distribution的转换
- 你的表述:
- 你提到通过“加入discounted future state distribution”来摆脱trajectory的summation形式,从而将问题转化为state的独立分布。
- 然后通过importance sampling,“通过除以old policy下的action distribution”将分布从new policy转为old policy。
- 评价:
- 正确部分:
- 你提到使用discounted state distribution(即状态访问频率 dπ(s))将轨迹上的回报总和转化为状态期望的形式,这是PPO理论推导中的一个关键步骤,非常正确。
- 你还提到了importance sampling,这也是PPO的核心技术,用于在旧策略采样的数据上估计新策略的期望。
- 不足之处:
- 在importance sampling的描述中,你说“除以old policy下的action distribution”是不准确的。正确的importance weight应该是新策略的动作概率除以旧策略的动作概率,即 πθold(a∣s)πθ(a∣s)。你的表述容易让人误解为直接用旧策略的分布做除法,而实际上这是一个比值(ratio)。
- 你提到的例子(City A和City B的身高调整)很好地类比了importance sampling的思路,但没有明确连接到PPO的公式,可能让读者感到不够具体。
dπ(s) d^{\pi}(s)
πθ(a∣s)πθold(a∣s)\frac{\pi_\theta(a|s)}{\pi_{\theta_{\text{old}}}(a|s)}
- 补充: 在PPO中,importance sampling的权重 πθold(a∣s)πθ(a∣s) 用于调整旧策略采样的动作,使其反映新策略下的期望。这个比值被称为importance weight,确保我们可以用旧数据近似新策略的表现。
πθ(a∣s)πθold(a∣s)\frac{\pi_\theta(a|s)}{\pi_{\theta_{\text{old}}}(a|s)}
(2) State Distribution的转换
- 你的表述: 你提到“假设state distribution差不多相同”,并“加入KL差来惩罚distribution的过大差异”。
- 评价:
- 正确部分:
- 你正确指出PPO假设新旧策略下的状态分布(state distribution)相近。这是PPO推导中的一个近似假设,因为如果状态分布差异过大,importance sampling的估计会变得不准确。
- 提到KL散度(KL divergence)来控制分布差异,也符合PPO的设计理念。
- 不足之处:
- 你说“加入KL差来惩罚”是PPO的一种实现方式(PPO-penalty),但在最常用的PPO变体(PPO-clip)中,并没有直接在loss函数中加入KL惩罚项,而是通过clipping机制间接限制新旧策略的差异。你可能混淆了PPO的两种变体。
- “差不多相同”的表述有些模糊,没有解释为什么可以做这个假设(例如,新旧策略的更新步长较小,导致状态分布变化不大)。
- 补充: 在PPO中,为了让状态分布的近似假设成立,算法限制了策略更新的幅度。PPO-clip通过裁剪(clipping)importance weight来实现这一点,而PPO-penalty则直接在目标函数中加入KL散度的惩罚项。两种方法都旨在保持新旧策略的相似性。
总结
优点
- 你对PPO的基本思想有一定的把握,特别是将问题分解为action和state的分布转换,并尝试用importance sampling和状态分布的概念解释其工作原理。
- 你提到的一些关键点(如从trajectory到state的转化、KL散度的作用)显示了你对算法背后逻辑的思考。
不足
- 细节不准确:
- importance sampling的weight表述错误,应为 πθold(a∣s)πθ(a∣s),而不是“除以old policy”。
- 对PPO的clipped objective和KL penalty的区别不够清晰,容易让人误解PPO的实现方式。
πθ(a∣s)πθold(a∣s)\frac{\pi_\theta(a|s)}{\pi_{\theta_{\text{old}}}(a|s)}
- 表达模糊:
- 一些概念(如“loss func可独立于最新的policy”“state distribution差不多相同”)没有充分展开,缺乏具体的数学或逻辑支持。
- 逻辑衔接不足:
- 你提到的问题(如on-policy的局限性)和解决方法(如importance sampling)之间的因果关系没有完全讲清楚。
建议
- 深入细节:建议仔细阅读PPO的原始论文(例如Schulman et al., 2017),特别是surrogate objective的具体公式和推导过程,澄清importance sampling和clipping的作用。
- 改进表达:在描述数学概念时,可以直接引用公式(如 πθold(a∣s)πθ(a∣s)),并结合具体例子解释其意义。
πθ(a∣s)πθold(a∣s)\frac{\pi_\theta(a|s)}{\pi_{\theta_{\text{old}}}(a|s)}
- 实践验证:尝试通过代码实现PPO算法(或阅读开源实现,如OpenAI Baselines),加深对理论的理解。
最终评价
你的学习成果值得肯定,尤其是对PPO核心思想的把握已经初具雏形。但要真正理解PPO公式,还需要在细节准确性和逻辑清晰度上进一步努力。继续加油,通过理论和实践的结合,你一定能更深入地掌握这个算法!
- Author:ran2323
- URL:https://www.blueif.me//article/1a771a79-6e22-80a9-897c-e3d80bd6aa89
- Copyright:All articles in this blog, except for special statements, adopt BY-NC-SA agreement. Please indicate the source!





